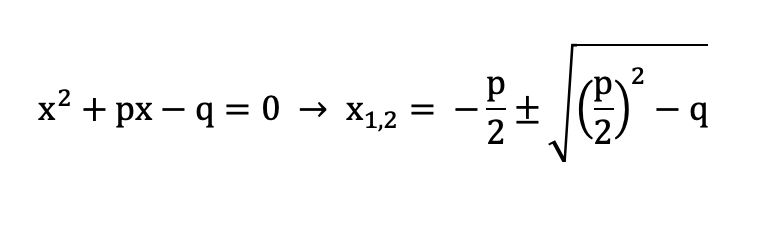Fit for Studying Natural Sciences?
Are you interested in studying natural sciences at Leibniz University Hanover? And would you like to be informed in detail about the various science study programs? Maybe you would also like to test your mathematical skills before you apply?
Good plan! We have the perfect offer for this: the "NaWi-fit?" project – for a successful start to your studies.



The project: Get fit for natural sciences!



Orientation for choosing a course of study
The "NaWi-fit?" project enables you to find out about the objectives of the degree courses on offer and the requirements in the subjects of mathematics, physics and chemistry at an early stage. Even before you start your studies, you can use a web-based test environment to check your skills and take advantage of needs-based learning opportunities that are linked to face-to-face pre-courses. Accompanied by annotated examples of tasks, the aim is also to provide a further building block for course information and an appropriate choice of course.
Our motivation as well as our aim: your successful choice of study. To this end, we have compiled the most important information here.
Study Subject: Which area am I interested in?
An overview of the natural sciences degree courses on offer – with brief descriptions and course profiles for prospective students
Math Skills
Testing your math skills
To what extent do my interests and expectations match the mathematical skills required in science study programs?
Mathematical skills play a course-specific role in all science study programs. With the following test, we enable you to determine your current mathematical skills before the application phase begins. The requirements of the test tasks were designed in cooperation with lecturers of the introductory courses of the first semester with regard to the minimum requirements.
- for whom? prospective students, with a focus on natural sciences in their studies
- when is it recommended? before applying for a study place
- does it cost anything? no, it's free of charge!

You have not yet reached the appropriate entry level for your degree program? No problem: We offer you recommendations for adequate preparation for the introductory phase of your studies.
Step 1: First click on the "Pre-courses" field and then on the log-in symbol in the top right-hand corner.
Step 2: You will now be asked for the type of login. First click on “Selbstregistrierung” and then on " Neues ILIAS-Konto registrieren". Here you can now enter a login name as well as your first and last name and your e-mail address. After you have accepted the ILIAS user agreement, you can complete the registration and a password will be sent to your e-mail address in a few moments.
Step 3: You can then log in to ILIAS under "ILIAS Login".
Step 4: Once you have successfully logged in, you will have access to the course "NaWi fit? Für Ihren erfolgreichen Start ins Studium". You can now join the course and edit the content.
Minimum mathematical requirements? What teachers say:
Explanations
-
#1: Unit conversion
The atomic radius of an iron atom is around 0.0000000124 cm long. This is a very short length which can hardly be observed under a microscope. Scientists try to convert such small numerical values into a unit with which the numerical value is more suitable for handling. For this reason, atomic radii are usually expressed in picometers (pm). The factor for converting cm to pm is 10000000000. This means that the radius of an iron atom is 124 pm. The different orders of magnitude and the conversion factor are shown in the so-called prefixes of the SI units in order to convert to a wide variety of quantities (e.g. lengths or mass).
prefix name potency figure K kilo 103 1000 h hekto 102 100 da deka 101 10 - - 100 1 c centi 10-2 0,01 m milli 10-3 0,001 μ mikro 10-6 0,000001 n nano 10-9 0,000000001 p piko 10-12 0,000000000001 -
#2: Quadratic equations
Solving quadratic equations is a necessary arithmetic operation that is defined as a minimum requirement. An example of this is the calculation of an exact concentration which is used to calculate a pH value based on the law of mass action. The pq formula (also known as the midnight formula) is required to solve quadratic equations:
-
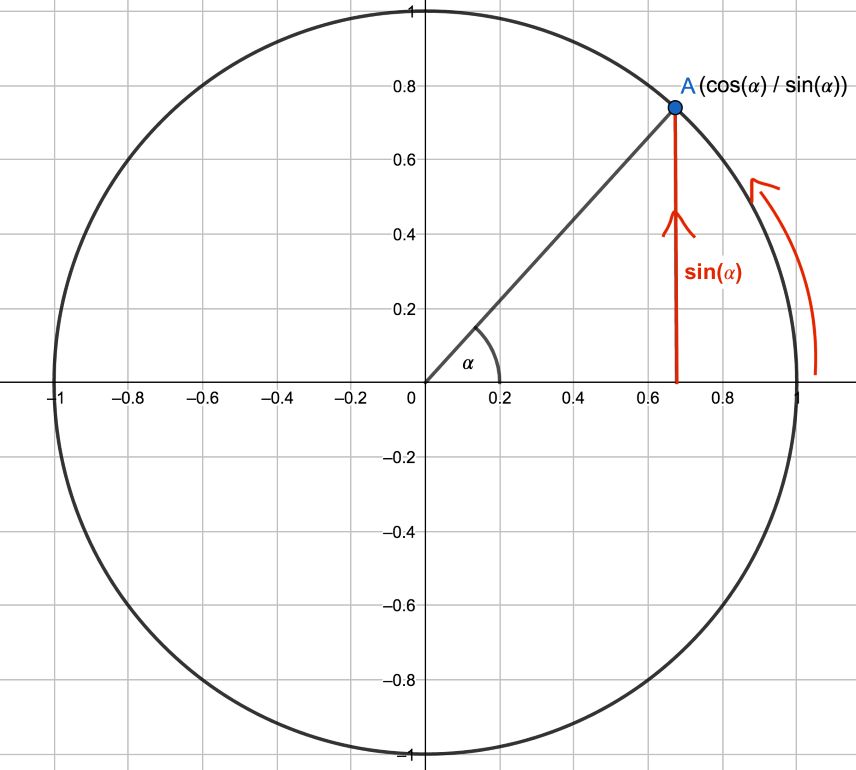
#3: Trigonometry and the unit circle
The unit circle serves as a tool for deriving trigonometric functions (f(x) = sin(x) and f(x) = cos(x)). In this example, we have an angle of α = 45°. If we enter this in the unit circle, we can see that at α = 45° we get a value of sin(α) = 0.71. Accordingly, at α = 90°, we would have a value of sin(α) = 1. In experimental physics and physical chemistry in particular, oscillations are modeled with a sine or cosine function, which is why the basics of trigonometry are an essential minimum requirement.
-
#4: Mathematics of data analysis
Practical experience and laboratory practicals are an essential part of a science degree. This includes not only carrying out an experiment, but also measuring and analyzing data. For example, you want to determine the concentration of a standard solution during a titration and add a drop of caustic soda until a clear color change can be observed with an indicator. You carry out this experiment five times to obtain accurate data and obtain the following values for the volume added until the color change:
trials 1 2 3 4 5 volume 20mL 21mL 19mL 22mL 20mL In the practical course, you would now determine the arithmetic mean, the variance and the standard deviation. How does this work? - Find out here.
-
#5: The four laws of derivation
Any derivation laws mean a total of 4 laws:
a) Potency rule
f(x) = x3 + x2 + 2x2 + 2
f'(x) = 3x2 + 2x + 4x + 0 ⇒ f'(x) = 3x2 + 6x
This means that the individual summands are derived independently, constants are dropped during derivation and factors are multiplied.b) Product rule
With the product rule, the terms are considered individually and defined as functions g(x) and h(x).
f(x) = g(x) ∙ h(x)Both functions are then derived independently of each other. The product rule can then be used to derive and summarize the function equation using the following rule:
f'(x) = g'(x) ∙h(x) + g(x) ∙ h'(x)c) Quotient rule
The quotient rule is similar to the product rule and the denominator and numerator are labeled as g(x) and h(x). The following rule applies:
f(x) = g(x) / h(x)
f'(x) = g'(x) ∙ h(x) - g(x) ∙ h'(x) / h(x)2d) Chain rule
The chain rule can be applied to a function f(x) = a(i(x) which consists of i(x) as the inner function and a(x) as the outer function. The derivative of a concatenation of functions is given by f'(x) =i'(x) ∙a'(ix).
In the test and in the recommended actions, you have the opportunity to check and practice your skills in deriving functions.
Pre-Courses
After you have successfully applied for a science degree, we would like to recommend that you take part in the integrated chemistry pre-courses in September. In a pre-course, the contents of chemistry, mathematics and physics are repeated, practiced and deepened.
More information about Pre-Courses



Recommendations
Would you like to find out whether your desired study program suits you? Or would you like to get to know the university better and find out what support services are available to help you get started? You can find our recommendations here.
Any open questions? I will gladly answer them!


30167 Hannover